
Dans le deux cas, on doit effectuer une division dont le diviseur est la mesure de l'hypoténuse du triangle rectangle considéré.
Question : quelle doit être la valeur du diviseur pour que la division soit la plus facile à effectuer ?
Réponse : si le diviseur de cette division vaut l'unité, alors le quotient est égal au dividende.
On va donc être amené à placer le point M (extrémité de l'hypoténuse du triangle rectangle OHM) à une distance de une unité du point O. Alors l'hypoténuse OM devient le rayon d'un quart de cercle du centre O.
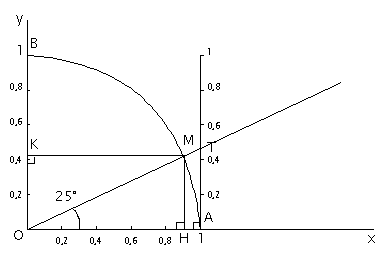
Lorsque le rayon OM tourne autour du point O, les angles AÔM prennent toutes les valeurs entre 0° et 90° (M se déplace de la position OA, à la position OB sur l'arc 'AB.)
Graduons OA unité graphique en dixièmes d'unités. On retrouve pour l'angle aigu de 25° la valeur approchée trouvée précédemment.
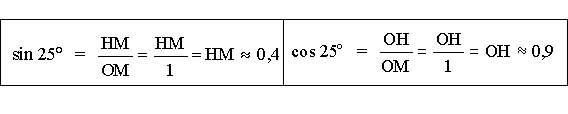
Nous pouvons dès lors donner une nouvelle définition du sinus et du cosinus d'un angle aigu (sans faire appel à la notion de triangle rectangle).
Nous constatons, sur la figure que nous venons de construire, que le cosinus de l'angle AÔM est l'abscisse du point M ; le sinus de l'angle AÔM est l'ordonnée du point M, par rapport à un système hortogonal xÔy :
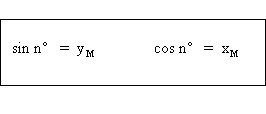
Remarque : la mesure de l'angle de n° peut être confondue avec la mesure de l'arc qu'il intercépte.
On parlera indifféremment de l'angle AÔM ou de l'arc 'AM.
Puisqu'il n'y a plus référence à un triangle rectangle et à des rapports entre ses côtés, on abandonnera la notion de rapports trigonométriques et on parlera de « lignes trigonométriques ».
Et la tangente, me direz-vous ? Dans le triangle rectangle utilisé plus haut, on avait donné comme définition :
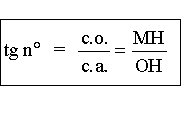
Là aussi, il convient de rechercher le calcul le plus aisé et donc de s'arranger pour avoir un dénominateur égal à l’unité. Ce qui nous conduit à utiliser le triangle rectangle AOT ; AT étant la portion de la droite tangente au cercle au point A comprise entre A et le prolongement du rayon OM en T.
Nous savons que le rapport
Remarque : le mot tangente a maintenant une double signification :
Pour l'angle de 25°, nous lisons sur la demi-droite AT : tg n° 0,5
Un nouvel aspect de la notion d'angle : Nous avons considéré, un peu plus haut, que le rayon OM tournait autour de O depuis A jusqu'en B en donnant ainsi toutes les valeurs comprises entre 0° (M confondu avec A) et 90° (M confondu avec B).
L'angle AÔM qui varie ainsi par « rotation » de OM est appelé angle de rotation et noté sous le symbole (OA,OM) et possèdera donc un côté origine OA (fixe) et un côté extrémité OM (mobile).
Extension de la notion d'angle de rotation
Considérons une roue de bicyclette dont l'axe O est immobile. Et privilégions un rayon OM. Faisons coïncider ce rayon OM avec l'horizontale à droite Ox.

Donnons une implusion à la roue. Au bout
d'un certain nombre de tours, la roue va
s'immobiliser en M ou en M'.
Donc le sens de rotation n'est pas
indifférent. Il va falloir déterminer les deux sens de
rotation pour éviter toute ambiguïté et pour cela
choisir un sens de rotation positif et un sens de
rotation négatif.
On a choisi comme sens positif celui qui
est inverse du sens de rotation des aiguilles d'une
montre à aiguilles.
d'un certain nombre de tours, la roue va
s'immobiliser en M ou en M'.
Donc le sens de rotation n'est pas
indifférent. Il va falloir déterminer les deux sens de
rotation pour éviter toute ambiguïté et pour cela
choisir un sens de rotation positif et un sens de
rotation négatif.
On a choisi comme sens positif celui qui
est inverse du sens de rotation des aiguilles d'une
montre à aiguilles.
Ce sens dit positif n'est pas arbitraire ; c'est celui de la rotation de la terre autour de son axe pour un observateur qui aurait les pieds au pôle sud et la tête au pôle nord. C'est aussi, mais parce que nous roulons à droite, le sens de rotation des voitures sur un rond-point routier.
Maintenant calculons quelques valeurs d'angles de rotations.
Imaginons que notre roue de bicyclette a fait 12 tours et s'est immobilisée de telle manière que le rayon OM soit à + 50° de OA. Quel est l'angle balayé par le rayon OM ?
360° x 12 +50° = 4320° + 50° = 4370°
Effectuer d'autres calculs et montrer que, d'une manière générale, un angle de rotation peut s'exprimer sous la forme :
(OA,OM) = n° + k x 360° O <= n <360°
Inversement, exprimer, sous la forme ci-dessus, un angle de rotation donné :
On constate qu'à chaque tour, les conditions initiales se retrouvent et que, par conséquent, la valeur n° a une importance particulière. On pourra l'appeler « représentant principal » de l'angle de rotation.
Ainsi, un plan orienté en « translation » par un repère orthonormé et en « rotation » comme défini ci-dessus, est totalement orienté et permet de définir totalement les déplacements.
le voilà enfin notre cercle trigonométrique, désigné sous une appellation fossile, qui, comme les restes d'animaux préhistoriques, porte un nom qui rappèle ses origines ;
on sait aussi la raison du rayon unitaire et de la rotation positive, raison due au souci de simplifier les calcule et à intégrer l'orientation locale à l'orientation universelle.
Et si nous le déroulions, ce cercle !
Qu'est-ce à dire ? Et bien, on peut imaginer que l'on coupe un cercle de tonneau et qu'on le met à plat ; ou bien qu'on déroule un fil inextensible qui entourait juste le cercle ; ou bien qu'on fait rouler le cercle sur une droite sans glisser, comme un cerceau, pour lui faire faire un tour complet.
Mais d'abord, il faut le graduer en degrés en choisissant de repérer les angles remarquables suivants et faciles à situer par construction géométrique, soit les angles suivants :
0° 30° 45° 60° 90° 120° 135° 150° 180° 210° 225° 240° 270° 300° 315° 330° 360°
[ Il conviendra de réaliser ces constructions sur une feuille annexe (voir feuille n°10) et de compléter cette feuille au fur et à mesure des explications. (L'idéal serait d'utiliser un papier millimétré, ou un papier quadrillé 5 mm.)
Calculons les longueurs des développements du cercle sur la droite support en se rappelant que le rayon du cercle vaut une unité. (Echelle utilisée 35 mm pour une unité).
Remarquons, pour faciliter le calcul, que
La longueur des arcs correspondants, à l'échelle choisie est de :
Il conviendra de continuer tous ces calculs et
de porter les mesures sur la droite sur laquelle
roule le cercle.
Revenons aux définitions obtenues plus haut :
Ces deux définitions peuvent, maintenant, s'appliquer pour un angle et pour un arc compris entre 0° et 360° ou entre 0 et 2? rad.
Il sera alors temps de prendre connaissance des équations et des fonctions trigonométriques sinus, cosinus et tangente en utilisant un abaque mobile constitué de la manière suivante.
Le fond de cet abaque sera constitué par une feuille de papier millimétré collé sur une feuille de carton assez rigide, le tout de format A4.
On notera sur ce fond, tous les renseignements utiles (axes des lignes trigonométriques, points et valeurs remarquables, graduations).
Une réglette rigide et transparente sera fixée au centre O du cercle trigonométrique de telle manière qu'elle puisse tourner autour du point O. Sur cette réglette sera fixée une équerre transparente au point M libre en rotation au point M.
Rotation autour du point O : une attache parisienne
Rotation autour du point M : un bouton pression
Un rapporteur gradué en radians
Pour le fabriquer il suffit de le coller sur une feuiie de caton fin, (genre ‘’bristol ‘’ puis de découpeer le pourtour et le profil.
Cet appareil peut servir à mesurer des angles et des axes exprimés en radians et surtout à calculer des longueurs d’arcs en remplaçant
la formule : par la formule ? (a, exprimé en radians.
