Objectif de la recherche lancée aujourd’hui avec la participation des apprenants :
REPRODUIRE UN ANGLE SUR UN AUTRE SUPPORT.
Voici, dessiné sur cette feuille de papier un secteur angulaire de 25° par exemple.
Problème : à l’aide de divers instruments, reproduire cet angle sur un autre support (mur, sol, planche, carton...).
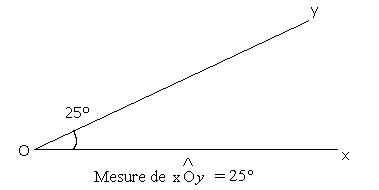
Instruments disponibles : rapporteur, papier calque, compas, équerre...
à l’aide du rapporteur ou du papier calque, pas de difficultés ;
à l’aide du compas ? Il suffit de mesurer la longueur de la corde qui sous-tend un arc ayant pour centre O et compris entre Ox et Oy.
Faites-le.
Mais quelle ouverture de compas faut-il prendre ?
Faites à votre idée, on verra bien !
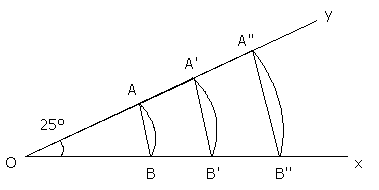
Voici, en exemples, trois relevés. Je constate que quelle que soit l’ouverture du compas, on obtient le même résultat.
La corde augmente de longueur de « la même manière » que l’ouverture du compas.
Vous avez déjà observé et peut-être étudié (formalisé) une telle situation.
Les longueurs telles que OA, OA’, OA’’ sont proportionnelles aux longueurs AB, A’B’ ,A’’B’’.
Avec une règle graduée, nous pouvons écrire :
Le rapport RAYON/CORDE est constant.
Si nous avions voulu reproduire un angle d’une autre mesure (35 ° par exemple), nous aurions constaté le même résultat, mais avec une autre valeur du rapport R/C.
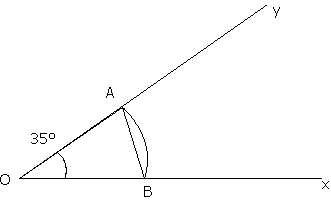
Pour l’angle de 35 ° le rapport R/C a pour valeur 3.3/2 = 1.65.
Le rapport ainsi établi est caractéristique de la mesure de l’angle considéré et cela est vrai pour tout angle compris entre 0 ° et 90 °.
Et enfin à l’aide d’une équerre :
Revenons à notre secteur angulaire de 25 ° et munissons-nous d’une équerre. Qu’est-ce qu’une équerre ? C’est un instrument servant à tracer des angles droits, à mener des perpendiculaires. C’est aussi l’image d’un triangle rectangle. Rappelons que le côté opposé à l’angle droit se nomme hypoténuse (du grec hypo qui signifie par dessous et du latin tenere qui veut dire tenir) hypoténuse : ce qui tient en-dessous.
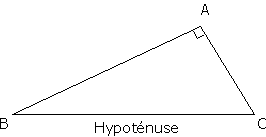
 angle droit
AB et AC côtés de l’angle droit
BC hypoténuse
Question :
Comment pouvons-nous disposer notre équerre à l’intérieur du secteur angulaire xÔy ?
Et bien, traçons des perpendiculaires aux côtés Ox et Oy de l’angle xÔy .
Limitons-nous à 3 perpendiculaires : 2 sur le côté Ox ; 1 sur le côté Oy.
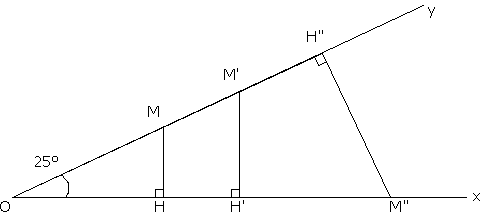
Les segments ainsi tracés délimitent, avec les côtés de l’angle xÔy, trois triangles rectangles.
Nommons-les : O H M O H’ ’M’ O H’’ ’M’’.
Constatons-nous, comme avec les arcs de cercle, des rapports de proportionnalité ?
Bien sûr, toutes ces mesures donnent des résultats approximatifs puisque les mesures sont toujours approchées. Mais enfin si tous les résultats convergent, ils constitueront un début de preuve. Notons un nombre aussi grand que possible de résultats.
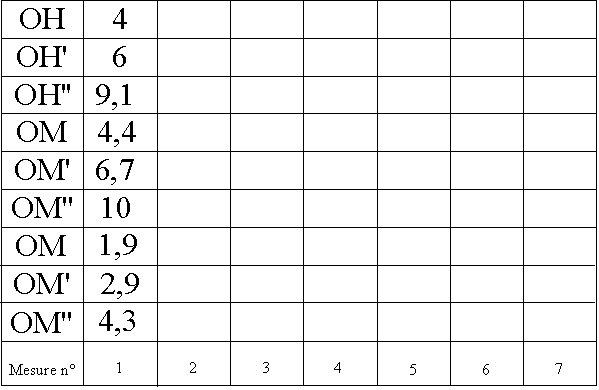
Il nous reste, maintenant, à calculer les rapports sur les séries de mesures.
Constatations : Quels que soient les triangles rectangles considérés, on constate que les rapports des côtés considérés sont constants (aux imprécisions de mesures près).
Ainsi, pour l’angle de 25 ° que nous avons tous tracé, et quel que soit le triangle rectangle considéré, nous avons les résultats suivants :
1 )
2 )
3 )
Prenons du recul
Nous avons, en définitive, et pour un angle aigu xÔy de valeur donnée, effectué des mesures de longueurs des côtés.
Nous avons effectué des mesures sur des triangles rectangles. Cette recherche (et toutes les conséquences que nous en tirerons par la suite) a reçu un nom.
On l’appelle TRIGONOMETRIE (tri pour trois; gone pour angle; métrie pour mesure : MESURES DANS LES TRANGLES).
Plus précisément (pour le moment) nous avons commencé l’étude de la :
TRIGONOMETRIE DANS LE TRIANGLE RECTANGLE;
Récapitulons et systématisons.
Soit un triangle rectangle donné.
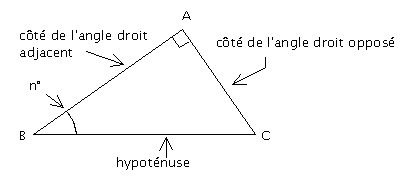
On appellera sinus de l’angle aigu B de n° le rapport entre le côté opposé et l’hypoténuse.
On appellera cosinus de l’angle aigu B de n° le rapport entre le côté adjacent et l’hypoténuse.
On appellera tangente de l’angle aigu B de n° le rapport entre le côté opposé et le côté adjacent.
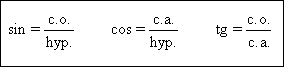
La signification des termes sinus, cosinus et tangente sera explicitée ultérieurement.
Puisque pour un angle aigu donné et quelles que soient les dimensions des triangles rectangles les rapports trigonométriques sont constants, on les a calculés une fois pour toutes et on a consigné les valeurs de ces rapports dans des tableaux appelés « tables des rapports trigonométriques d’un angle aigu. »
Il restera à distribuer ces tables à chacun des élèves et à pratiquer diverses lectures. Il sera notamment intéressant de connaître par cœur les rapports trigonométriques d’angles remarquables 30 ° 45 ° 60 °.
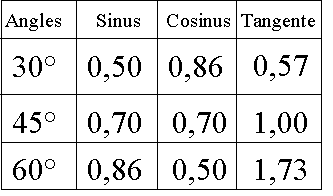
On remarquera que le sinus d’un angle aigu est égal au cosinus de son complément, et par application du théorème de Pythagore : sin² n° + cos² n° = 1.
Puisque les rapports trigonométriques d’un angle aigu sont des quotients (rapports) de deux des côtés d’un triangle rectangle, plusieurs types de calculs sont possibles :
connaissant la mesure des côtés d’un triangle rectangle, calculer la mesure de ses angles aigus;
connaissant la mesure d’un côté et d’un angle, calculer la mesure des autres côtés.
Il s’agit là d’un simple problème de division dans l’ensemble des décimaux.
Connaissant deux des éléments de cette division, calculer le troisième.
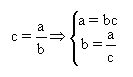
La seule difficulté consiste à choisir le bon quotient, en fonction des éléments connus :
le sinus fait intervenir le côté opposé et l’hypoténuse.
le cosinus fait intervenir le côté adjacent et l’hypoténuse.
la tangente fait intervenir le côté opposé et le côté adjacent.
Ce chapitre pourra être achevé par l’exécution de nombreuses applications.
